本文目录导读:
深入解析中序遍历:原理、步骤及应用
在数据结构与算法领域中,树的遍历是一个重要的概念,它指的是按照某种规则访问树中的每个节点,使得每个节点被访问且仅被访问一次,中序遍历是树遍历的一种重要方式,它在二叉树的操作中尤为常见,本文将详细解析中序遍历的原理、步骤及应用,帮助读者深入理解并掌握这一关键概念。
中序遍历的原理
中序遍历是指按照左子树、根节点、右子树的顺序遍历一棵二叉树,对于任意一棵二叉树,中序遍历的步骤如下:
1、首先遍历左子树,即按照中序遍历的规则遍历左子树的所有节点;
2、然后访问根节点;
3、最后遍历右子树,即按照中序遍历的规则遍历右子树的所有节点。
中序遍历的原理基于二叉树的递归性质,对于一棵非空二叉树,它的左子树和右子树本身也是二叉树,因此可以分别对它们进行中序遍历,通过递归地应用这一原理,我们可以实现对整棵二叉树的中序遍历。
中序遍历的步骤
下面我们将通过一个具体的例子来详细展示中序遍历的步骤,假设我们有一棵如下的二叉树:
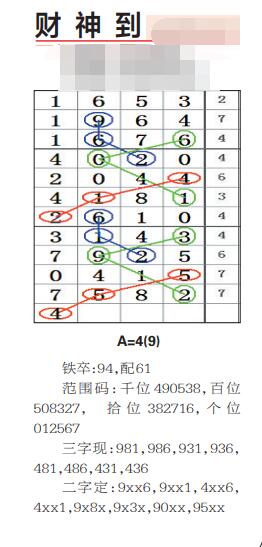
A
/ \
B C
/ \ \
D E F按照中序遍历的规则,我们应该首先遍历左子树,然后访问根节点A,最后遍历右子树,具体步骤如下:
1、遍历左子树:
- 左子树的根节点是B,我们需要继续遍历B的左子树;
- B的左子树只有一个节点D,直接访问D;
- 遍历完B的左子树后,访问B节点;
- 然后遍历B的右子树,右子树只有一个节点E,直接访问E。
2、访问根节点A。
3、遍历右子树:
- 右子树的根节点是C,我们需要继续遍历C的右子树;
- C的右子树只有一个节点F,直接访问F。
按照上述步骤,我们得到的中序遍历序列为:DBEAFC。
中序遍历的应用
中序遍历在二叉树的操作中具有广泛的应用,以下是几个典型的应用场景:
1、二叉搜索树的中序遍历:对于一棵二叉搜索树(BST),中序遍历可以得到一个升序的节点值序列,这是因为二叉搜索树的左子树包含所有小于根节点的值,右子树包含所有大于根节点的值,通过中序遍历,我们可以将二叉搜索树转换为一个有序的数组或列表,便于进行查找、插入和删除等操作。
2、表达式树的求值:在编译器设计中,表达式树是一种常见的数据结构,用于表示数学表达式,中序遍历可以用于计算表达式树的值,我们可以将运算符作为节点,操作数作为叶子节点,然后按照中序遍历的顺序依次访问节点,在访问运算符节点时,我们可以根据运算符和操作数计算出该节点的值,遍历完整个表达式树后,根节点的值即为整个表达式的计算结果。

3、线索二叉树:线索二叉树是一种对二叉树进行遍历优化的数据结构,在普通的二叉树中,空指针域没有得到有效利用,线索二叉树利用这些空指针域来存储指向节点在某种遍历次序下的前驱节点和后继节点的指针,通过中序遍历,我们可以将一棵普通的二叉树转换为线索二叉树,从而实现对二叉树的高效遍历。
中序遍历的实现方式
中序遍历的实现方式有多种,包括递归实现、迭代实现以及使用栈的辅助实现等,下面我们将分别介绍这些实现方式。
1、递归实现:递归实现中序遍历是最直观的方式,我们可以定义一个递归函数,该函数接受一个节点作为参数,并按照中序遍历的顺序访问该节点及其子节点,递归的终止条件是节点为空。
2、迭代实现:迭代实现中序遍历需要使用一个栈来辅助遍历过程,我们首先将根节点入栈,然后进入一个循环,直到栈为空,在循环中,我们不断将栈顶节点的左子节点入栈,直到找到一个没有左子节点的节点,我们访问该节点,并将其右子节点(如果存在)入栈,通过不断重复这个过程,我们可以实现中序遍历。
3、使用栈的辅助实现:这种实现方式结合了递归和迭代的思想,我们维护一个栈来保存待访问的节点,同时用一个指针来指向当前需要处理的节点,在遍历过程中,我们不断将当前








发表评论